Computing with the Fabric of Reality

by Chris Silva (a.k.a. Sarah Jane Smith)

This is an article in which I plan to describe quantum-based computers and their application for defeating public-key crypto.

Let's begin by describing basic quantum principle.  Particles work in funny ways.  It's believed that anything at the atomic scale obeys the laws of a very different type of physics than we normally see: quantum physics.

Unlike classical physics, quantum physics deals with information and probability instead of physical forces interacting.  For quantum-based computers all we really care about are particles in superposition, quantum entanglement, and quantum interference.

Particles in Superposition

A particle can have at least two different states, spin-up and spin-down (or 1 and 0).  That's all we care about right now.

Logically, one would think that a particle with two states is either in one or the other.  That isn't so.  Under quantum physics a particle is in both (or all possible states, given its location) at the same time.

That is, until the particle is observed, it's neither spin-up nor spin-down but both.

Quantum Entanglement and Non-Physical Communication

Quantum entanglement is when two interacting particles are in superposition.

Schrödinger's cat is a good example.  Say we have a particle in a chamber that either decays or does not.  In that chamber there's a Geiger counter that's hooked up to a device that releases a poison gas into another chamber that contains a cat.  Since both the particle and the cat are in chambers we cannot see them  We cannot observe the particle to see whether it has decayed or not, and we can't see the cat to reason what happened to the particle.

The cat, the particle, the Geiger counter, and the poison releasing device are said to be in superpositional entanglement (or quantum entanglement).  Only until we observe the cat, the reality where it died from the poison gas or the reality where it's still alive is our own.  Any time before we observe things, the cat is both alive and dead.

Although this example may not be too likely on account of the size of the cat and all, particles can become entangled in this way.  In fact, particles can become entangled in such a way as to allow non-physical communication.  Once in superpositional entanglement particles remain that way until observed, even if they move miles apart.

Say that we have two particles at 10:00p in superposition.  At 10:10p we put both of them into a device where they are XOR'd (remember: spin-down = 0, spin-up = 1) so that the particles come out of the device as both 0 or both 1, or rather, since they're in superposition they're both 0 and 1 at the same time.

Now we move them (in special containers that isolate them completely) to two labs: Alice's lab and Bob's lab.  They both get their particles at 11:00p.  Alice puts her particle into a device that changes it to a 1 without observing it (e.g. laser-cooling ion trap).  Bob sits still and does nothing.  At exactly 11:10.29p Bob and Alice observe the state of their particles.  They're both 1!  What this means is Alice communicated a 1 to Bob non-physically.  Since their particles were in superpositional entanglement until they both observed them at 11:10.29p, one affected the other's probability of being 1 when Alice put hers into her device.

Quantum Interference

Quantum interference is what makes most quantum-based computers possible.

All possibilities are thought to exist in different universes and, on a quantum level, a particular universe with a particular possibility only manifests itself in our own when observed.  There is no way to directly observe a possibility that is not our own, but we can do it indirectly!  Imagine that you're standing on a cliff.  There are basically two different things you can do.  You can either jump off or walk away.

You imagine yourself jumping off - you slam against the rocks at the bottom and die instantly.  Since you don't want to die, you walk away.  While you didn't jump off the cliff you imagined that you did   The frightening possibility of you slamming against those rocks interfered with you jumping off.  This sort of interference of possibilities can be demonstrated with a photon.

Figure 1:  A is a photon source that emits one photon, B and C are two detectors that can detect a single photon, and D is a semi-transparent mirror that, when only dealing with one photon, reflects or does not seemingly at random.

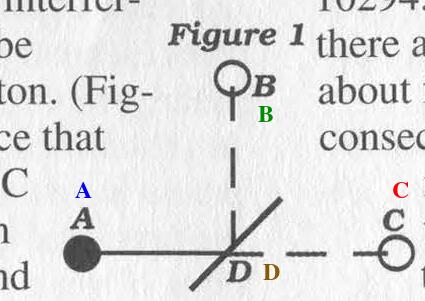
Logically, you would assume that both B and C have a 50 percent chance of detecting the photon because it went either one way or the other.  While the results are the same, this is not what happens.

When the photon strikes D it goes into a superposition of being reflected and not being reflected.  Since both possibilities can be observed, they both try to manifest into our own universe.  But the properties of D only allow one to.

So there's a 50/50 chance of it being detected by B or C.

Now, go to Figure 2:

We've placed a photon-stopping plate in the non-reflecting path.  Again, logically you would assume that the photon would have a 50 percent chance of being detected by B and a 50 percent chance of being stopped by the plate.

And again, this is not what happens.  But this time the results are not the same because of quantum interference.

Because only the possibility where the photon is reflected into B is observable, only that possibility becomes our own.  Therefore, there's a 100 percent chance that the photon ends up in B.  Man that's weird!

Better Things Will Surely Come Our Way

We have a million random numbers, each number being unique.

We are looking for the address of number 10,294.  Under traditional technology there are only two ways one can go about finding 10,294.  One way is to consecutively check all one million numbers until we come across the right one.

The other way is to do the same thing but divide our workload by adding more checkers.  Quantum-based computers do the latter, but in a very unique way.  They divide our workload amongst checkers existing in different universes.  As such, they have the capability of dividing work infinitely.

So let's build one, Figure 3:

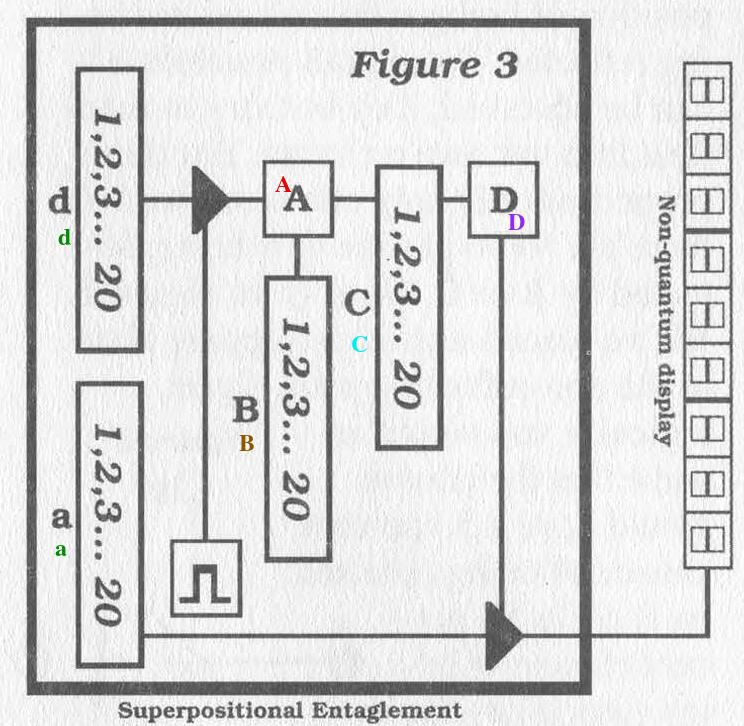
Classical memory cells (or bits) exist in two states, 1 and 0.  Our memory cells are individual particles and, as such, they obey quantum physics.  Since we're not observing them (at first) they're in the superposition of 1 and 0.  (A bit in superposition is called a qubit.)

Recall that Alice transmitted 1 to Bob by changing the state of her particle.  Bob's particle became 1 because it was physically impossible for it to be otherwise if Alice's was also 1 before observing it.  That little trick of reality allows us to store multiple numbers in the same physical memory.

Therefore, all one million 9-digit (or about 20-bit) numbers can be stored in only 40 qubits (actually only 20, but we want the address too).  If we changed the state (again, without observing it) of d0-19 to 0, d20 to 1, a0-a19 to 0, and a20 to 1 at the same time, we created a possibility for, depending on how you look at it, address 1 to equal 1.

We can repeat this one million times until we've stored all our random numbers.

The classical design of our system is to let whatever is in d be sent to A during each clock.

A compares its input with the number we're looking for, which is stored in register B.

A stores the bit addresses that are shared between B and its input in C (e.g. if bit-2 of the input and bit-2 of B are the same, store 1 in bit-2 of C).

D checks C to see if all bits equal one.  If they do, D switches on the gate to our non-quantum display which reads the contents of a.

This is what actually happens: During the first clock all possibilities stored in d are compared by A in different universes.

Physically only one possibility can exist, so in that universe similarities between input A and B are stored in C.

Since C is directly related to switching on our observable non-quantum display, that possibility starts to interfere with others because it's observable.

During the second clock, all non-observable possibilities stored in d are compared.

In other words, d possibilities that do not have the same bit correlations with B as stored in C in different universes are compared.

This is continued until there can only exist one possibility, we're looking at B in d, and that's when our display lights up with our answer!

That is quantum computing.

Really Practical Applications

The great majority of cryptography systems, especially public-key systems, depend either heavily or completely on the difficulty of factoring large numbers.

Quantum-based computers have the potential of reducing the predicted computing time of billions of years to mere seconds for factoring numbers of "secure" size.  If such a computer were built, all public-key crypto would become insecure.

So, let's build one:

The algorithm we intend to use for factoring is well known.  The number we wish to factor is called N.

We start off by taking a random number a between 0 and N.  We then figure out a phase r by computing:

int find_phase(int a, int N) { int tmpp, R[0xFFFF], r; for (tmpp = 0;; tmpp++) { R[tmpp] = pow(a, tmpp % N); if (test_repeat_store_in_r(R, &r)) break; } return r; }

After some time, R[tmpp] will start to repeat itself, test_repeat_store_in_r() returns true when this happens and stores the number of digits that repeat in r.

Then we take the greatest common divisors (Euclid's algorithm) of: (N, pow(a, r/2) + 1) and (N, pow(a, r/2) - 1)

The result of this is the two factors of N.

Computing r under classical means is very slow.  For increasing digits of N the computation time increases exponentially.

The only thing our quantum computer is concerned with is computing r.  The rest of the factoring can be done normally.

We have two registers in superposition, x and k.

x and k are not prepared so that there exists the possibilities for x and k to be any numbers between: 0 and pow(2, sizeof(int) * 8)

We then compute: k = pow(a, x) % N

(Which is a part of find_phase() above.)

After that we perform t = k, where t is some non-quantum register.

Because pow(a, x) % N has the same return value for x + i * r, where i is any number, x is in superposition of all numbers that equal k.

(Remember, we read k by: t = k      [k is no longer in superposition].)

We are now ready to read x.  There's a slight possibility that: x = t

If this happens, we'll have to perform the operation again.  If x != t, we have: r = abs(t - x)

Now that we've found r in no time we can compute the greatest common divisors of (N, pow(a, r/2) + 1) and (N, pow(a, t/2) - 1) with a classical computer.  This should take very little time.

The advantages of such a computer are obvious.  Its potential for breaking public key crypto may be balanced by non-physical communication transferring secret keys about.

Still, with huge increases in memory and theoretical infinite parallelism we'll be able to do amazing things.

My theory about the books 3001: The Final Odyssey is that the black monolith was a small computer with the capability of simulating entire worlds.  That LSD trip Dave had at the end of 2001: A Space Odyssey was him entering it.

Now, is such a computer that far off?