|
Lo primero que voy a hacer es
repasar todo el algoritmo de verificación del serial desde el principio,
de modo que se pueda tener una mejor perspectiva a la hora de afrontar
la protección en su conjunto.
Bien, comencemos. En el menú de introducción de los datos
tenemos un cuadro de edición para introducir el nombre, y justo
debajo aparece un código deducido a partir de las caracteristicas
de nuestra máquina (que es el número de volumen del disco
duro). Más abajo tenemos el cuadro de edición para introducir
el número de serie.
Si colocamos un breakpoint en función GetWindowTextA comprobamos
que el programa se interrumpe 3 veces, presumiblemente por los tres datos
para verificar el serial. Traceando a partir de la tercera interrupción
llegamos a una serie de instrucciones muy interesantes, en concreto en
la direccin 43A69D:
(NOTA: no voy a explicar instrucción a
instrucción que es lo que hacen las rutinas ya que parto de que
hay un mínimo de conocimientos, a parte de que el lector debería
ser quien analizara por su cuenta los algoritmos con la ayuda de este texto.)
:0043A69D 8A03
mov al, byte ptr [ebx] ; EBX es un puntero
al serial
:0043A69F 84C0
test al, al
:0043A6A1 741A
je 0043A6BD
:0043A6A3 8BF3
mov esi, ebx
:0043A6A5 8B8D34020000
mov ecx, dword ptr [ebp+00000234]
:0043A6AB 2C30
sub al, 30 ; A todos los caracteres se les
resta 0x30, de modo que los caracteres
:0043A6AD 50
push eax ; deberan
tener un valor igual o superior a 0x30.
:0043A6AE E89DFB0000
call 0044A250 ; Se realiza un
algoritmo que veremos despues.
:0043A6B3 8806
mov byte ptr [esi], al ; Se sustituye
el valor antiguo
:0043A6B5 8A4601
mov al, byte ptr [esi+01]
:0043A6B8 46
inc esi
:0043A6B9 84C0
test al, al
:0043A6BB 75E8
jne 0043A6A5
Ahora vamos a ver en detalle el algoritmo de la dirección 44A250:
:0044A250 8A4C2404
mov cl, byte ptr [esp+04]
:0044A254 32C0
xor al, al
:0044A256 84C9
test cl, cl
:0044A258 7C05
jl 0044A25F
:0044A25A 80F909
cmp cl, 09
:0044A25D 7E29
jle 0044A288
:0044A25F 80F910
cmp cl, 10
:0044A262 7C0D
jl 0044A271
:0044A264 80F92A
cmp cl, 2A
:0044A267 7F08
jg 0044A271
:0044A269 80E906
sub cl, 06
:0044A26C 8AC1
mov al, cl
:0044A26E C20400
ret 0004
:0044A271 80F92F
cmp cl, 2F
:0044A274 7505
jne 0044A27B
:0044A276 B025
mov al, 25
:0044A278 C20400
ret 0004
:0044A27B 80F931
cmp cl, 31
:0044A27E 7C0A
jl 0044A28A
:0044A280 80F94A
cmp cl, 4A
:0044A283 7F05
jg 0044A28A
:0044A285 80E90B
sub cl, 0B
:0044A288 8AC1
mov al, cl
:0044A28A C20400
ret 0004
Aqui se realizan toda una serie de comparaciones de lo mas sencillas.
De modo que en función del valor introducido devuelve uno u otro.
Pero la inversión de este algoritmo la veremos mas tarde, de momento
sigamos viendo que más se hace.
Ahora que hemos pasado la primera fase del algoritmo general, sigamos
traceando. Un poco mas adelante nos encontramos con otro bucle que trabaja
sobre el número de serie anteriormente modificado.
:0043A6EA 85FF
test edi, edi
:0043A6EC 7C1E
jl 0043A70C
:0043A6EE 8B8D34020000
mov ecx, dword ptr [ebp+00000234]
:0043A6F4 8D543C6C
lea edx, dword ptr [esp+edi+6C]
:0043A6F8 52
push edx ; Puntero a un
buffer vacio
:0043A6F9 53
push ebx ; Inicialmente
puntero a los últimos 4 datos del serial
:0043A6FA E891FB0000
call 0044A290
:0043A6FF 83EE04
sub esi, 00000004
:0043A702 83EB04
sub ebx, 00000004
:0043A705 83EF03
sub edi, 00000003
:0043A708 85F6
test esi, esi
:0043A70A 7DDE
jge 0043A6EA
Lo que se realiza aqui es transformar grupos de 4 bytes en 3 bytes,
de modo que si el serial tiene 8 bytes, este quedará en otro de
6 bytes. Hay que tener en cuenta que este empieza por el final. Como he
dicho antes, mas adelante nos encargaremos de invertir la función
de la dirección 44A290, la cual lo único que hace es pasar
un algoritmo que a partir 4 bytes se deduzcan los valores de 3 bytes.
Mas tarde, en la dirección 43A741 se hace una copia del nombre
de usuario a un buffer vacio que esta justo antes del buffer donde se ha
modificado el número de serie. Inmediatamente despues se coge el
número de la máquina y se copia sobre el nombre de usuario.
Veamoslo:
:0043A741 56
push esi ; Pumtero del nombre
de usuario
:0043A742 50
push eax ; Puntero del buffer
vacio
:0043A743 E868A20700
call 004B49B0 ; Aqui se
realiza la copia
:0043A748 8B8D34020000
mov ecx, dword ptr [ebp+00000234]
:0043A74E 8BFE
mov edi, esi
:0043A750 33C0
xor eax, eax
:0043A752 83C40C
add esp, 0000000C
:0043A755 8B9184010000
mov edx, dword ptr [ecx+00000184] ;Coge
el número de la maquina
:0043A75B 83C9FF
or ecx, FFFFFFFF
:0043A75E 8954244C
mov dword ptr [esp+4C], edx ;
Lo copia sobre el nombre de usuario
Ahora se realiza una serie operaciones XOR para sacar un valor a partir
del nombre de usuario original:
:0043A762 B2AA
mov dl, AA ;Valor inicial
del registro DL
:0043A764 F2
repnz
:0043A765 AE
scasb
:0043A766 F7D1
not ecx
:0043A768 49
dec ecx ;
Se saca la longitud del nombre de usuario
:0043A769 85C9
test ecx, ecx
:0043A76B 7E0A
jle 0043A777
:0043A76D 8A1C06
mov bl, byte ptr [esi+eax] ;
Puntero al nombre de usuario
:0043A770 32D3
xor dl, bl
; Operación XOR
:0043A772 40
inc eax
:0043A773 3BC1
cmp eax, ecx
:0043A775 7CF6
jl 0043A76D
:0043A777 3A94248C000000 cmp dl, byte ptr
[esp+0000008C] ; Comparación
de validación
:0043A77E 0F85A6000000
jne 0043A82A
La comprarción que se realiza en la direccion 43A777 sirve para
de alguna manera validar del número de serie, sería algo
asi como la primera prueba de autenticidad. Lo que hace es comparar el
valor obtenido de las operaciones XOR del nombre de usuario con el 4º
valor empezando por el final del serial modificado en el ultimo paso. Para
que el serial sea válido tiene que darse la condición de
que sean iguales. Ya tenemos una condición del serial.
A continuación se llama a una función que recibe como
parametros un buffer vacio de una longitud de 20 bytes, los 3 últimos
caracteres deducidos del número de serie modificados, y el presumiblemente
un 3 indicando la longitud de estos últimos 3 caracteres.
:0043A786 8D4C2424
lea ecx, dword ptr [esp+24]
:0043A78A 89442424
mov dword ptr [esp+24], eax
:0043A78E 51
push ecx ; Buffer de 20
bytes
:0043A78F 8944242C
mov dword ptr [esp+2C], eax
:0043A793 8D942491000000
lea edx, dword ptr [esp+00000091]
:0043A79A 89442430
mov dword ptr [esp+30], eax
:0043A79E 6A03
push 00000003
:0043A7A0 89442438
mov dword ptr [esp+38], eax
:0043A7A4 52
push edx ; Tres últimos
bytes del serial modificado
:0043A7A5 89442440
mov dword ptr [esp+40], eax
:0043A7A9 E82268FFFF
call 00430FD0
Si ejecutamos el call, en el buffer de los 20 bytes obtenemos un resultado.
Vamos a ver en que consiste este algoritmo:
:00430FD0 83EC5C
sub esp, 0000005C
:00430FD3 8D442400
lea eax, dword ptr [esp]
:00430FD7 50
push eax ; Puntero a zona
de memoria de variables
:00430FD8 E8D3DBFFFF
call 0042EBB0 ; Inicialización
de las variables
:00430FDD 8B4C2468
mov ecx, dword ptr [esp+68]
:00430FE1 8B542464
mov edx, dword ptr [esp+64]
:00430FE5 51
push ecx ; Longitud del
mensaje
:00430FE6 8D442408
lea eax, dword ptr [esp+08]
:00430FEA 52
push edx ; Puntero al mensaje
:00430FEB 50
push eax ; Zona de memoria
de variables y padding
:00430FEC E8EFDBFFFF
call 0042EBE0
:00430FF1 8B542478
mov edx, dword ptr [esp+78]
:00430FF5 8D4C2410
lea ecx, dword ptr [esp+10]
:00430FF9 51
push ecx ; Puntero a zona
de variables y padding
:00430FFA 52
push edx ; Puntero a digest
:00430FFB E8E0FEFFFF
call 00430EE0 ; Algoritmo
y padding
:00431000 83C474
add esp, 00000074
:00431003 C3
ret
En la primera llamada se inicializan unas variables a unos valores muy
concretos, veamos cuales són:
:0042EBB6 C70001234567
mov dword ptr [eax], 67452301
:0042EBBC C7400489ABCDEF
mov [eax+04], EFCDAB89
:0042EBC3 C74008FEDCBA98
mov [eax+08], 98BADCFE
:0042EBCA C7400C76543210
mov [eax+0C], 10325476
:0042EBD1 C74010F0E1D2C3
mov [eax+10], C3D2E1F0
Si no tenemos mucha idea de los algoritmos de
encriptación estos valores no nos dirián nada, pero para
aquel al que le suene el algoritmo Hash
SHA-1, se dará cuenta de que estos son precisamente los valores
de inicialización para realizar el algoritmo. Ahora que intuimos
(por que todavía no es seguro) a que nos enfrentamos, voy a hacer
una pequeñisima mención de lo que es el algoritmo SHA-1.
Se trata de una función Hash de una única vía, lo
cual quiere decir que una vez aplicado el algoritmo no es posible deducir
cual es el plaintext
a partir del ciphertext,
a menos que se utilice la fuerza bruta. Esto es debido a que utiliza funciones
no lineales. Estos producen una salida llamada
digest
o hash de un
número constante de bits, dependiendo del algoritmo. Mientras que
la longitud de la entrada es variable, ya que esta se convierte a una cadena
de un numero constante de bits. A este proceso se le llama padding.
Estos algoritmos inicialemente se pensaron como funciones de compresión,
pero se pueden utilizar para firmas digitales asi como para proteger programas.
No voy a explicar las operaciones que se realizan dentro del algoritmo.
Para mas información leer un documento sobre criptografia.
La salida del algoritmo SHA-1 es de 160 bits, mientras que la longitud
del mensaje despues del proceso padding es de 512 bits. Una vez explicado
muy por encima el SHA-1, vamos a intentar identificar las diferentes fases.
La función que se ejecuta en la direccion 430FEC realiza una
copia del mensaje sobre la zona de memoria donde se va a realizar el proceso
de padding. Es en la tercera funcion (430FFB) donde se concluye con el
proceso de padding y se aplica el algoritmo propiamente dicho:
:00430F32 6A01
push 00000001
:00430F34 6814B45100
push 0051B414
:00430F39 56
push esi
:00430F3A E8A1DCFFFF
call 0042EBE0
:00430F3F 8B4E14
mov ecx, dword ptr [esi+14]
:00430F42 83C40C
add esp, 0000000C
:00430F45 81E1F8010000
and ecx, 000001F8
:00430F4B 81F9C0010000
cmp ecx, 000001C0 ; Rellena
de ceros hasta los primeros 448 bits
:00430F51 75DF
jne 00430F32
El resto de los 64 bits es la longitud en bits del mensaje, la cual
se copia en las siguientes lineas:
:0042EC25 8B742418
mov esi, dword ptr [esp+18]
:0042EC29 2BE8
sub ebp, eax
:0042EC2B 8D7C181C
lea edi, dword ptr [eax+ebx+1C]
:0042EC2F 8BCD
mov ecx, ebp
:0042EC31 8BC1
mov eax, ecx
:0042EC33 C1E902
shr ecx, 02
:0042EC36 F3
repz
:0042EC37 A5
movsd
Ahora por último el algoritmo propiamente dicho se encuentra
en la dirección 430EC44
:0042EC42 51
push ecx
:0042EC43 53
push ebx
:0042EC44 E857000000
call 0042ECA0
Donde recibe como parametros el mensaje de 512bits y las variables inicializadas.
Todo el tratamiento consiste en realizar 80 funciones no lineales obteniendo
un resultado de 160 bits que se suma a los valores iniciales que hemos
visto antes.
Ahora ya tenemos claramente identificado el algoritmo SHA-1 dentro de
la proteccion. Es bueno realizar pruebas con algoritmos implementados y
comparar resultados con mensajes comunes, ya que nunca se sabe si el programador
a modificado alguna variable u operación dentro del algoritmo, lo
cual no deberia extrañarnos.
Para implementar el keygen deberemos de conseguir una implementacion
del algoritmo, o por el contrario se la puede hacer uno mismo, pero sinceramente
es una matada.....
:0043A7AE 8B442430
mov eax, dword ptr [esp+30] ;
Primeros 4 bytes
:0043A7B2 8B4C2434
mov ecx, dword ptr [esp+34] ;
Siguientes 4 bytes
:0043A7B6 33D2
xor edx, edx
:0043A7B8 89442424
mov dword ptr [esp+24], eax ;
Copia de los primeros 4 bytes
:0043A7BC 89542444
mov dword ptr [esp+44], edx
:0043A7C0 894C2428
mov dword ptr [esp+28], ecx
; Copia de los siguientes 4 bytes
Lo que se ha obtenido son 160 bits, que seran utilizados mas adelante.
Aunque de principio los 8 primeros bytes se guardan en diferentes zonas
de memoria.
:0043A7D6 50
push eax
:0043A7D7 81C1A4110000
add ecx, 000011A4
:0043A7DD 89542454
mov dword ptr [esp+54], edx
:0043A7E1 6A10
push 00000010
:0043A7E3 51
push ecx
:0043A7E4 89542460
mov dword ptr [esp+60], edx
:0043A7E8 E8E367FFFF
call 00430FD0
Aqui se vuelve a utilizar el algoritmo SHA-1 donde se encriptan 16 bytes
constantes y se obtiene un resultado de 160 bits tambien constante (lògicamente).
Esto último no se por que el autor lo haría, supongo que
como una medida para despistar.
Mensaje: E4 05 1E 00 E5 F0 BC A5 4A 71 01 DA
37 21 A4 7D
Digest: BC DA 16 7E 85 33
39 54 B0 E1 C8 5A AA 07 F0 53 18 F7 CF 31
A continuación (43A7FC) se pasa como parametros el resultado
obtenido de SHA-1, su longitud, y una dirección. Aparantemente no
ocurre nada, pero sigamos ejecutando instrucciones. Inmediatamente despues
nos encontramos con una función que recibe hasta 6 parámetros.
Pero sigamos ejecutando instrucciones.
:0043A7F8 52
push edx ; Puntero resultado
digest
:0043A7F9 6A14
push 00000014 ; Longitud
digest
:0043A7FB 50
push eax ; Puntero desconocido
:0043A7FC E8AFDAFCFF
call 004082B0
:0043A801 8D4C243C
lea ecx, dword ptr [esp+3C]
:0043A805 6A00
push 00000000
:0043A807 8D9424DC000000
lea edx, dword ptr [esp+000000DC]
:0043A80E 51
push ecx ; Puntero a los
8 primeros bytes del digest del serial
:0043A80F 52
push edx ; Puntero desconocido
:0043A810 8D8424C0000000
lea eax, dword ptr [esp+000000C0]
:0043A817 6A20
push 00000020
:0043A819 8D8C24A0000000
lea ecx, dword ptr [esp+000000A0]
:0043A820 50
push eax ; Puntero buffer
vacio
:0043A821 51
push ecx ; Puntero a la
ultima transformacion del serial
:0043A822 E8B9CCFCFF
call 004074E0
Tras la ejecución de la función de la dirección
43A822 se obtiene un resultado sobre el buffer vacio. Pero si continuamos
un poco mas adelante vemos como se realizan unas series de comparaciones
que prometen ser muy interesantes.
:0043A82A 8B84240C110000
mov eax, dword ptr [esp+0000110C]
:0043A831 85C0
test eax, eax
:0043A833 7425
je 0043A85A
........
:0043A85A B908000000
mov ecx, 00000008
; Se comparan 8 dwords
:0043A85F 8D7C244C
lea edi, dword ptr [esp+4C] ;
Puntero al nombre de usuario con el número de la
; maquina superpuesto
:0043A863 8DB42490000000
lea esi, dword ptr [esp+00000090] ;
Resultado de la llamada en 43A882
:0043A86A 33D2
xor edx, edx
:0043A86C F3
repz
:0043A86D A7
cmpsd
:0043A86E 7427
je 0043A897
Se deduce que para que el registro sea valido los 64 bytes deben ser
iguales. Ahora ya tenemos mas o menos claro el objetivo, vamos a adentrarnos
en las funciones de las direcciones 43A7FC y 43A882.
Empezando con la funcion de la dirección 43A7FC, recibe tres
parametros, lo que podría ser un buffer, el resultado de la segunda
pasada del algoritmo SHA-1, que como recordaremos se trataba de una serie
de bytes constantes. Y por ultimo un numero 0x14, que podria ser la longitud
de esta ultima que he comentado. Si nos metemos dentro, lo primero que
nos encontramos es una copia de datos desde una dirección de la
seccion .data (los cuales podemos suponer que seran constantes) a la direccion
que ha recibido como parámetro. El número total de dwords
que copia es 0x412.
:004082B3 B912040000
mov ecx, 00000412 ; Número
de dwords a copiar
:004082B8 53
push ebx
:004082B9 8B5C2410
mov ebx, dword ptr [esp+10] ;
Puntero a buffer
:004082BD 56
push esi
:004082BE 57
push edi
:004082BF BE60045100
mov esi, 00510460 ; Origen
de los datos
:004082C4 8BFB
mov edi, ebx
:004082C6 F3
repz
:004082C7 A5
movsd
Inmediatamente despues se hace toda una serie de operaciones que modifican
toda la tabla utilizando los valores del resultado de la segunda pasada
del algoritmo SHA-1 de longitud 20 bytes.
Si miramos detenidamente el contenido de la tabla inicial podemos identificar
los valores como los P-arrays iniciales y los S-Boxes iniciales del algoritmo
de encriptación Blowfish. Esto último se puede verificar
examinando la documentación del algoritmo en cuestión. Ahora
ya tenemos una posible idea del algoritmo que usa. Se pueden verificar
todas las operaciones, bien comparandolas con alguna implementación
valida (podemos suponer que esto sería la inicialización
del algoritmo), o sino comparando el resultado de las dos inicializaciones.
Si aceptamos el hecho de que se trata de un algoritmo Blowfish, deducimos
que el resultado de la segunda pasada del algoritmo SHA-1 es la llave de
encriptacion, la cual es constante, como es logico.
Lo que se consigue aqui es una expansión de la llave (sub-llaves)
hasta un total de 4168 bytes, con 18x4 bytes para los P-arrays y 4x4x256
bytes para los S-Boxes. Los pasos a seguir a la hora crear las sub-llaves
para aquel que desea verificarlo serían los siguientes:
-
Inicializar los P-arrays y los S-Boxes con los valores fijos de inicialización.
-
Realizar la operación XOR con P1 (32 bits) y el primer dword de
la llave, luego entre P2 y los siguientes 32 bits de la llave, hasta P18.
Cuando los bits de la llave se acaben, volver a repetirlo ciclicamente.
-
Encriptar un plaintext de valor 0 con blowfish utilizando las sub-llaves
anteriormente deducidas.
-
Reemplazar P1 y P2 por el ciphertext obtenido.
-
Se vuelve a encriptar el resultado de la anterior con las sub-llaves modificadas.
-
Se vuelven a reemplazar P3 y P4, volviendose a repetir el ciclo hasta modificar
los P-arrays y las S-Boxes.
El algoritmo de encriptación Blowfish, tambien denominado como block
cipher, encripta en bloques de 64 bits, con una llave de tamaño
variable de hasta 448 bits. Se trata de un algoritmo simétrico debido
a que la llave de encriptación sirve tanto para encriptar como para
desencriptar.
Vamos ahora con la segunda función, que teniendo en cuenta la
lista de parametros que recibe debe de tratarse de la encriptación
o desencriptación del número de serie modificado, al cual
le asigna una longitud de 0x20 bytes.
Podemos ver como le da la vuelta, por decirlo de alguna manera, a los
dwords obtenidos de los 8 primeros bytes del resultado del algoritmo SHA-1
del serial, y los guarda en otras variable.
........
:0040778E 89442410
mov dword ptr [esp+10], eax ;
Primeros 4 bytes
........
:004077BB 894C2438
mov dword ptr [esp+38], ecx ;
Siguientes 4 bytes
........
:0040783A 52
push edx
:0040783B 50
push eax
:0040783C 46
inc esi
:0040783D 896C2424
mov dword ptr [esp+24], ebp ;
Primetos 4 bytes a encriptar/desencriptar
:00407841 895C2428
mov dword ptr [esp+28], ebx ;
Siguientes 4 bytes a encriptar/desencriptar
:00407845 E8E6010000
call 00407A30
Lo mismo se hace con los 8 primeros bytes del array a encriptar/desencriptar
y se guardan en los registros EBP y EBX. A continuación se llama
a una función. Hay que tratar de averiguar si se trata de una encriptación
o una desencriptación.
Para ello primero vamos intentar entender dichos algoritmos. Como he
dicho antes, la operación se realiza en bloques de 64 bits, dando
un resultado tambien de 64 bits. Ambas operaciones (encriptación/desencriptación)
consisten en un bucle de 16 repeticiones, como indica el siguiente diagrama
de bloques:
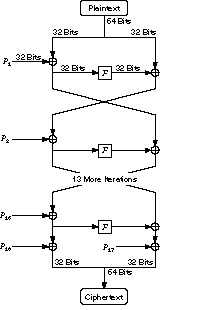 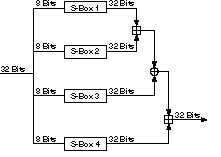
Encriptación
Los parametros P se refieren a los P-arrays que antes se han obtenido
a partir de la llave, asi como los S-Box son las S-Boxes obtenidas también
antes. Se trata de realizar 16 iteraciones con los 64 bits, y en cada iteración
se realiza la funcion F descrita en la parte derecha, donde la entrada
de 32 bits se divide en 4 bloques de 8 bits, que representan el indice
de entrada a las tablas de las S-Boxes, un byte para cada tabla, es decir,
cuatro tablas de 256 entradas cada una.
El byte de menor peso entra en la tabla S-Box4 y el de mayor peso en
la tabla S-Box1. La unica difenrencia entre el algoritmo de encriptacion
y desencriptacion esta en que en la desencriptación los parametros
P se empiezan a utilizar desde P18 hasta P1, que es justo al reves que
en la encriptacion.
Sin mas, ya podemos empezar el algoritmo para ver de que se trata. La
primera llamada al algoritmo estaría aqui.
:00407E7E 8B5044
mov edx, dword ptr [eax+44] ;
Coge P18 de la tabla de P-arrays
:00407E81 33CA
xor ecx, edx ; Operación
XOR entre P18 y parte baja del dato a desencriptar
:00407E83 33D2
xor edx, edx
:00407E85 8BD9
mov ebx, ecx
:00407E87 894C2418
mov dword ptr [esp+18], ecx ;
Guarda resultado de la operacion
:00407E8B 8A54241A
mov dl, byte ptr [esp+1A] ;
Recoge los bits 16-23 del resultado.
:00407E8F C1EB18
shr ebx, 18 ; Se queda con
los bits 24-32 del resultado.
:00407E92 8B949048040000
mov edx, dword ptr [eax+4*edx+00000448] ;
Entra en la tabla S-Box2
:00407E99 8B6C9848
mov ebp, dword ptr [eax+4*ebx+48] ;
Entra en la tabla S-Box1
:00407E9D 33DB
xor ebx, ebx
:00407E9F 8ADD
mov bl, ch ; Recoge los
bits 8-15 del resultado
:00407EA1 03D5
add edx, ebp ; Suma resultados
de S-Box1 y S-Box2
:00407EA3 8BAC9848080000 mov ebp,
dword ptr [eax+4*ebx+00000848] ;
Entra en la tabla S-Box3
:00407EAA 8BD9
mov ebx, ecx
:00407EAC 81E3FF000000
and ebx, 000000FF ; Recoge
los bits 0-7 del resultado
:00407EB2 33D5
xor edx, ebp ; Operacion
XOR entre resuiltados S-Box3 y (S-Box1 + S-Box2)
:00407EB4 8BAC98480C0000 mov ebp, dword
ptr [eax+4*ebx+00000C48] ;
Entra en la tabla S-Box4
:00407EBB 03D5
add edx, ebp ; Obtiene resultado
de función F
:00407EBD 8B6840
mov ebp, dword ptr [eax+40] ; Coge P17 de la tabla de
P-arrays
:00407EC0 33D5
xor edx, ebp ; En estas
dos operaciones XOR se empieza con la siguiente iteración
:00407EC2 33F2
xor esi, edx ;
Aqui se realiza el cambio de nibbles.
:00407EC4 33D2
xor edx, edx
:00407EC6 89742418
mov dword ptr [esp+18], esi
.........
Esto sería el código correspondiente a una de las iteraciones,
en concreto a la primera. Y examinando el código llegamos a la conclusion
de que se trata de una desencriptacion, entre otras cosas debido a que
se empieza por P18. Fijarse como se realiza el cambio de la parte baja
por la alta del dato de 64 bits que estan guardados en ESI y ECX.
Antes de seguir quisiera apuntar un detalle acerca de la funcion que
reside en la direccion 407A30, la cual se encargaba
de desencriptar los datos. Pues si os fijais recibe un tercer parametro
que es un cero. Si examinais el codigo vereis que es lo primero que se
verifica, debido a que es el flag que determina si se trata de una encriptacion
o una desencriptacion.
:00407830 6A00
push 00000000
Ahora ya tenemos claro que se trata de una desencriptación, veamos
que se hace con los resultados. Normalmente este tipo de encriptaciones
no se realizan encriptando los bloques de 64 bits independientemente uno
del otro. Existen varios modos de funcionamiento:
-
CBC: El ciphertext es obtenido mediante la operacion XOR entre el plaintext
del bloque actual y el resultado de ciphertext del bloque anterior, para
luego encriptar el resultado.
-
CFB: El ciphertext se obtiene encriptando el ciphertext del bloque anterior
y despues realizando la operacion XOR entre el resultado y el plaintext
del bloque actual.
Veamos que método utiliza el caso que tenemos entre manos.
:0040783A 52
push edx
:0040783B 50
push eax
:0040783C 46
inc esi
:0040783D 896C2424
mov dword ptr [esp+24], ebp
; Primeros 32 bit ciphertext
:00407841 895C2428
mov dword ptr [esp+28], ebx ;
Siguientes 32 bit ciphertext
:00407845 E8E6010000
call 00407A30 ; Se desencripta
:0040784A 8B44241C
mov eax, dword ptr [esp+1C] ;
Primeros 32 bit del resultado SHA-1
:0040784E 8B4C2424
mov ecx, dword ptr [esp+24]
; Primeros 32 bit desencriptados
:00407852 8B542428
mov edx, dword ptr [esp+28]
; Siguientes 32 bit desencriptados
:00407856 33C1
xor eax, ecx ; Resultado
final desencriptacion de 32 bit primeros
:00407858 8B4C2444
mov ecx, dword ptr [esp+44] ;
Siguientes 32 bit del resultado SHA-1
:0040785C 83C40C
add esp, 0000000C
:0040785F 33CA
xor ecx, edx ; Resultado
final desencriptación de 32 bit siguientes
Luego el resultado final se utiliza para desencriptar el siguiente bloque,
y asi hasta el final. Con esta información deberiamos ser capaces
de deducir que el modo utilizado es el CBC. Al encriptar/desencriptar el
primer bloque no se tiene el ciphertext del bloque anterior, de modo que
en este caso el programador ha utilizado los primeros 64 bit del resultado
del algoritmo SHA-1 de los tres ultimos bytes del numero de serie modificado.
Y finalmente el resultado de la desencriptación se compara con
el nombre de usuario, como se ha visto antes.
De todo esto podemos sacar la longitud que debe tener el número
de serie. El array que se desencripta y compara es de 32 bytes. A estos
hay que sumarle el byte del checkeo mediante XOR, y los tres bytes que
se pasan por SHA-1 para obterner los 8 bytes para el modo CBC de blowfish.
Suman un total de 36 bytes, que teniendo en cuenta el algoritmo que pasa
de 4 a 3 bytes, tenemos un numero de serie de longitud 36*4/3 = 48 bytes
Ya se ha descrito todo el proceso de verificación del serial,
ahora voy dar los pasos que se deben seguir para realizar el keygen que
cree los números de serie validos:
-
Generar la cadena de 32 bytes con el nombre de usuario y el número
de la máquina superpuesto.
-
Generar aleatoriamente los tres últimos bytes del serial modificado
por la función 44A290 para pasarlos por el algoritmo SHA-1 y asi
conseguir los 8 bytes para encriptar en modo CBC.
-
Aplicar el algoritmo SHA-1 sobre estos tres bytes.
-
Calcular el 4º byte empezando por el final del serial modificado mediante
el algoritmo de la dirección 43A762 sobre
el nombre de usuario.
-
Encriptar mediante Blowfish con la llave conocida
el nombre de usuario con el número de la maquina superpuesto. El
tamaño del plaintext debe de ser de 32 bytes, para ello rellenar
en resto con ceros. Antes de pasar por el encriptador y despues de pasar
por el hay que recordar que tenemos que dar la vuelta a los dwords, es
decir, el byte de menor peso pasa a ser el de mayor y viceversa.
-
Concatenar los 32 bytes resultantes con los otros
4 deducidos al principio.
-
Aplicar la inversa del algoritmo de la direccion
44A290.
-
Aplicar la inversa del algoritmo de la direccion
44A250.
Y estos serían los pasos que habría
que dar para conseguir realizar un keygen para esta aplicación.
Hasta ahora debería estar claro el poder realizar todos los pasos
excepto los dos ultimos, aunque estos poco tienen que ver con la encriptación,
solo es cuestión de tener un poco de imaginación.
Segun mi experiencia, el algoritmo mas complicado
de los dos es el de la dirección 44A290, el encargado de pasar 4
bytes a 3 bytes.
:0044A290 53
push ebx
:0044A291 56
push esi
:0044A292 8B74240C
mov esi, dword ptr [esp+0C]
:0044A296 57
push edi
:0044A297 0FBE4E02
movsx ecx, byte ptr [esi+02]
; Coge el tercer byte
:0044A29B 8A5E03
mov bl, byte ptr [esi+03] ;
Coge el cuarto byte
:0044A29E 8A4601
mov al, byte ptr [esi+01]
; Coge el segundo byte
:0044A2A1 8BF9
mov edi, ecx ; EDI = tercer
byte
:0044A2A3 83E13F
and ecx, 0000003F
:0044A2A6 83E33F
and ebx, 0000003F
:0044A2A9 8AD0
mov dl, al ; EDX = segundo
byte
:0044A2AB C1E106
shl ecx, 06 ; Desplaza tercer
byte 6 bit a la izquierda
:0044A2AE 0BD9
or ebx, ecx ; Operacion
OR entre cuarto byte y tercero modificado
:0044A2B0 8A0E
mov cl, byte ptr [esi] ;
Coge el primer byte
:0044A2B2 C0F804
sar al, 04 ; Rotacion del
segundo byte 4 bits a la derecha
:0044A2B5 83E23F
and edx, 0000003F
:0044A2B8 2403
and al, 03
:0044A2BA C1FF02
sar edi, 02 ; Rotacion del
tercer byte 2 bits a la derecha
:0044A2BD C0E102
shl cl, 02
:0044A2C0 C1E204
shl edx, 04
:0044A2C3 83E70F
and edi, 0000000F
:0044A2C6 0AC1
or al, cl
:0044A2C8 8B4C2414
mov ecx, dword ptr [esp+14]
:0044A2CC 0BD7
or edx, edi
:0044A2CE 5F
pop edi
:0044A2CF 5E
pop esi
:0044A2D0 885902
mov byte ptr [ecx+02], bl
; Tercer nuevo byte
:0044A2D3 8801
mov byte ptr [ecx], al ;
Primer nuevo byte
:0044A2D5 885101
mov byte ptr [ecx+01], dl ;
Segundo nuevo byte
:0044A2D8 5B
pop ebx
:0044A2D9 C20800
ret 0008
Nada mas empezar podemos deducir el valor del
primer byte de los cuatro:
PRIMERO_4
= PRIMERO_3 >> 2 (El "subindice" indica
si pertenece al grupo de 3 o 4 bytes)
Esto es debido a que PRIMERO_3 es el resultado de la operación
OR entre AL y CL, pero CL proviene de la rotación a la izquierda
de PRIMERO_4. Como la operación es una OR podemos suponer que CL=AL,
de modo que PRIMERO_4 es la rotación de 2 bits a la derecha de PRIMERO_3.
AUX = PRIMERO_3 & 0x3
__asm sal AUX , 4
AUX = AUX | ((SEGUNDO_3)>>4)
SEGUNDO_4=AUX
A pesar de que hemos dicho antes que CL=AL, no
podemos sin embargo suponer que AL=CL, debido a que AL viene impuesto con
la regla de que todos sus bit excepto los tres de menor deben ser cero.
Esta condicion hace que la igualdad no se de en los dos sentidos, de modo
que a PRIMERO_3 le aplicamos la operacion AND con el valor 0x03.
Una vez hecho esto, realizamos sobre este valor
una rotación de 4 bits a la izquierda. Pero todavía no podemos
asegurar que este valor corresponda a SEGUNDO_4, debido a que antes de
hacer nada con SEGUNDO_4, este se guarda en el registro DL. El cual se
desplaza 4 bits a la izquierda y su resultado se asigna a SEGUNDO_3. De
modo que para que se den las dos condiciones inversas, tiene que existir
una relacion entre SEGUNDO_3 y PRIMERO_3 con SEGUNDO_4.
Esta relación la conseguimos mediante
la operación OR entre el resultado de la inversión a partir
de SEGUNDO_3 y el de la inversión a partir de PRIMERO_3. Esto se
debe a que cuando se hace una rotación en el algoritmo hacia la
derecha y hacia la izquierda, en realidad nos quedamos con la parte alta
y baja del byte. Al hacer la inversa tenemos que juntar los dos resultados,
y eso lo hacemos con la operación OR.
CUARTO_4 = (TERCERO_3) &
0x3f
El cuarto número sale directamente debido
a que no hay operaciones muy complejas por medio.
AUX = SEGUNDO_3 & 0x0F
__asm sal AUX , 2
TERCERO_4 = AUX
AUX = (TERCERO_4) & 0x0C0
AUX = AUX>>6
TERCERO_4 = (TERCERO_4) |
AUX
Esto es algo mas complicado. Aqui ocurre algo parecido que con el caso
de SEGUNDO_4. Empezamos invirtiendo una rama desde SEGUNDO_3 mediante una
operación AND y una rotación a la izquierda de 2 bits, de
modo que recuperamos los 6 bits de mayor peso. Ahora tenemos que recuperar
los dos bit de menor peso, para ello hacemos una AND para coger los dos
bits de mayor peso del resultado anterior y hacemos un desplazamiento de
6 bits hacia la derecha. Para juntar los dos resultados utilizamos la operación
OR.
Ya tenemos invertido uno de los dos algoritmos, ahora queda el mas facil,
el de la direccion 44A250.
:0044A250 8A4C2404
mov cl, byte ptr [esp+04] ;
Recordar que previamente se le ha restado 0x30
:0044A254 32C0
xor al, al
:0044A256 84C9
test cl, cl
:0044A258 7C05
jl 0044A25F
:0044A25A 80F909
cmp cl, 09
:0044A25D 7E29
jle 0044A288
:0044A25F 80F910
cmp cl, 10
:0044A262 7C0D
jl 0044A271
:0044A264 80F92A
cmp cl, 2A
:0044A267 7F08
jg 0044A271
:0044A269 80E906
sub cl, 06
:0044A26C 8AC1
mov al, cl
:0044A26E C20400
ret 0004
:0044A271 80F92F
cmp cl, 2F
:0044A274 7505
jne 0044A27B
:0044A276 B025
mov al, 25
:0044A278 C20400
ret 0004
:0044A27B 80F931
cmp cl, 31
:0044A27E 7C0A
jl 0044A28A
:0044A280 80F94A
cmp cl, 4A
:0044A283 7F05
jg 0044A28A
:0044A285 80E90B
sub cl, 0B
:0044A288 8AC1
mov al, cl
:0044A28A C20400
ret 0004
Analizando el código anterior podemos particionar un rango de
números de 0 a 0x4A en 6 condiciones:
[0,9] -> No cambia
]9,0x2A] -> Resta 6
{0x2F} -> Fuerza a 0x25
]0x2A,0x31[ -> Fuerza a cero
]0x4A,inf [ -> Fuerza a cero
[0x31,0x4A] -> Resta 0xB
Si invertimos las relaciones de esta tabla llegamos a los siguiente:
[0,9] -> No cambia
[0xA,0x24] -> Suma 6
{0x25} -> Fuerza a 0x2F
[0x26,0x3F] -> Suma 0xB
Al resultado final hay que sumarle el valor 0x30, y ya tenemos el serial
definitivo. Un poco largo, verdad? Pues ahora queda lo mas facil, programar
el keygen. Para ello debemos conseguir implementaciones de libre distribución
ya realizadas de los algoritmos Blowfish y SHA-1, a menos de que se disponga
de ganas y tiempo y se desee hacer la propia implementación de los
algoritmos. Yo he optado por implementaciones en C, entre otras cosas por
que son los más difundidos. Una buena base de datos la podeis encontrar
en ftp.funet.fi
Para los que no quieran buscar, las implementaciones que yo he usado
las puede coger desde aquí los ficheros para el algoritmo Blowfish
y SHA-1.
A continuación voy a poner el listado de las funciones del algoritmo
del keygen, ya se que esta un poco chapucero, pero es lo que hay, y ya
no tenia demasiadas ganas de mejorarlo.
#include <stdio.h>
#include "blowfish.h"
#include "sha1.h"
char nombre[255]="Mr. YelloW";
unsigned int cod=0x12345;
unsigned char serial[49];
int stime;
long ltime;
void Algoritmo (void);
int Intercambia (int num);
void Algo (unsigned char *ori,unsigned char *dest);
void Algoritmo (void) {
BLOWFISH_CTX ctx;
unsigned char key[]={0x0bc,0x0da,0x016,0x07e,0x085,0x033,0x039,0x054,0x0b0,0x0e1,0x0c8,0x05a,0x0aa,0x07,0x0f0,0x053,0x018,0x0f7,0x0cf,0x031};
SHA1_CTX context;
unsigned char digest[20], codigo[3];
unsigned char plaintext[32];
unsigned int *pti;
unsigned int xorl,xorr,tmpl,tmpr;
unsigned char final[36];
unsigned char *ori;
unsigned char *dest;
char chk;
unsigned int cod;
int i=0,len;
// Generación numeros aleatorios
ltime = time (NULL);
stime = (unsigned) (ltime/(rand()+1));
srand(stime);
codigo[0]=0x30+(rand())%10;
codigo[1]=0x30+(rand())%10;
codigo[2]=0x30+(rand())%10;
for(i=0;i<32;i++)
plaintext[i]=0;
// Nombre de usuario con código máquina
superpuesto
strcpy(plaintext,nombre);
pti=(unsigned int *)plaintext;
*pti=cod;
// Algoritmo SHA1
SHA1Init(&context);
SHA1Update(&context, codigo, 3);
SHA1Final(digest, &context);
pti=(unsigned int *)digest;
xorl=*pti;
xorr=*(pti+1);
xorl=Intercambia(xorl);
xorr=Intercambia(xorr);
// Algoritmo Blowfish
Blowfish_Init (&ctx, key, 0x14);
pti=(unsigned int *)plaintext;
// Rotacion
*pti=Intercambia(*pti);
*(pti+1)=Intercambia(*(pti+1));
*(pti+2)=Intercambia(*(pti+2));
*(pti+3)=Intercambia(*(pti+3));
*(pti+4)=Intercambia(*(pti+4));
*(pti+5)=Intercambia(*(pti+5));
*(pti+6)=Intercambia(*(pti+6));
*(pti+7)=Intercambia(*(pti+7));
// Encriptación modo CBC
for(i=0;i<4;i++) {
tmpl=*pti;
tmpr=*(pti+1);
*pti=*pti^xorl;
*(pti+1)=*(pti+1)^xorr;
Blowfish_Encrypt(&ctx,
pti, pti+1);
xorl=*pti;
xorr=*(pti+1);
*pti=Intercambia(*pti);
// Se vuelven a rotar
*(pti+1)=Intercambia(*(pti+1));
pti=pti+2;
}
// Generación byte chequeo
chk=0x0AA;
len=strlen(nombre);
for(i=0;i<len;i++)
chk=chk^nombre[i];
for(i=0;i<32;i++)
final[i]=plaintext[i];
final[32]=chk;
final[33]=codigo[0];
final[34]=codigo[1];
final[35]=codigo[2];
// Inversa algoritmo 44A290
ori=final;
dest=serial;
for(i=0;i<12;i++) {
Algo(ori,dest);
ori=ori+3;
dest=dest+4;
}
serial[48]=0;
// Inversa algoritmo 44A250
for(i=0;i<48;i++) {
len=serial[i];
if((len>=0)&&(len<=9))
{
serial[i]=serial[i]+0x30;
continue;
}
if((len>=10)&&(len<=0x24))
{
serial[i]=serial[i]+0x06;
serial[i]=serial[i]+0x30;
continue;
}
if((len>=0x26)&&(len<=0x3f))
{
serial[i]=serial[i]+0x0B;
serial[i]=serial[i]+0x30;
continue;
}
if(len==0x25) {
serial[i]=0x2f;
serial[i]=serial[i]+0x30;
continue;
}
}
}
int Intercambia (int num) {
int aux;
aux=(num&0x0ff)<<24;
aux=aux + ((num&0x0ff00)<<8);
aux=aux + ((num&0x0ff0000)>>8);
aux=aux + ((num&0x0ff000000)>>24);
return(aux);
}
void Algo(unsigned char *ori,unsigned char *dest)
{
unsigned int edi_,al_;
*dest=*ori >> 2;
al_=(*ori)&0x3;
__asm sal al_,4;
al_=al_|((*(ori+1))>>4);
*(dest+1)=al_;
edi_=*(ori+1)&0x0f;
__asm sal edi_,2;
*(dest+2)=edi_;
edi_=(*(ori+2))&0x0c0;
edi_=edi_>>6;
*(dest+2)=(*(dest+2))|edi_;
*(dest+3)=(*(ori+2))&0x3f;
}
En caso de que alguien este interesado en el tema y desee leer mas acerca
de la criptografia, puede pasarse por las siguientes urls donde encontrara
información de los diferentes algoritmos, implementaciones y libros.
Cryptography
page by James Pate Williams, Jr.
SSH - Tech
Corner - Cryptographic Algorithms
Pagina The Egoiste
Estas son algunas de las tantas páginas y quizas no de las mejores
dedicadas a la criptografía, pero es un comienzo.
Bueno, pues por el momento esto ha sido todo.
Hasta el próximo tutorial!!!
Agur.
|