
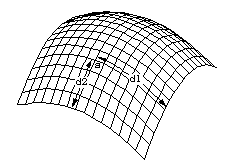
Oder ein Polarsystem zu verwenden (wieder zwei Angaben: Länge und Winkelgröße).
| Schema | D | Erklärung |
 |
1 | Jeder Punkt A auf einer 1-dimensionalen Kurve kann durch genau eine Zahl eindeutig dargestellt werden, durch die Länge "d" vom Ausgangspunkt. |
 |
2 |
Jeder Punkt A auf einer 2-dimensionalen Oberfläche kann durch genau zwei Zahlen
eindeutig dargestellt werden. Eine von vielen Methoden ist, auf die Oberfläche
ein "Gitter" zu projizieren und die Längen der Gitterlinien zu messen. Oder ein Polarsystem zu verwenden (wieder zwei Angaben: Länge und Winkelgröße). |
 |
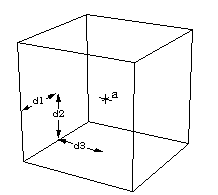
3 | Jeder Punkt A im 3-dimensionalen Raum kann durch genau drei Zahlen eindeutig definiert werden. Üblicherweise werden dazu die drei Ordinaten X, Y und Z verwendet. |

 |
Wird dieser Prozeß, genannt "Iteration" unendlich oft weitergeführt, so entsteht ein Fraktal.
Dies wird an mehrere Sachen deutlich, zum ersten kann bei unendlicher Iteration
ein Punkt auf der Form nicht mehr eindeutig durch eine Zahl beschrieben werden,
obwohl die Form nur aus eindimensionalen Objekten (s.o.) besteht, da die Form
unendlich lang ist (Bei jeder Iteration wird die Summe der Längen aller Strecken
mit 4/3 multipliziert). Diese Form schafft es also, eine unendliche Länge
auf begrenztem Raum "aufzustauen", ohne sich dabei selbst zu schneiden. |
| Fraktale Geometrie | Euklidische Geometrie |
|---|---|
| neuzeitliche Erfindung | traditionell |
| keine bestimmende Länge oder Vergrösserung | basiert auf festen Grössen |
| trifft auf viele natürliche Objekte zu | trifft eher auf von Menschen erschaffene Objekte zu |
| durch einen Algorithmus beschrieben | durch eine Formel beschrieben |
| Typ | Grafik | Erklärung | ||
|---|---|---|---|---|
| "Einfache Fraktale" |  |
Einfache Fraktale (ich wusste keinen anderen Namen) entstehen aus einfachen Bildungsregeln, wie z.B. die Koch-Schneeflocke oder das links dargestellte Sierpinski-Dreieck, bei dem das gleichseitige Dreieck in vier kongruente Dreiecke unterteilt wird und immer das "mittlere" herausgenommen wird. (Sierpinski Dreieck: D ~= 1.5849...). | ||
| Chaotische Systeme |  |
Jedem Bildpunkt wird ein Punkt in der Gausschen Zahlenebene zugewiesen,
diese komplexe Zahl wird dann iteriert, d.h. in eine Formel eingesetzt, und der
entstehende Wert wieder in die Formel eingesetzt, dies geschieht solange,
bis entweder die Zahl konvergiert, zwischen mehreren Zahlen springt oder gegen unendlich
strebt. Je nach dem Resultat erhält der Bildpunkt dann eine Farbe (hier
Schwarz für konvergierte Werte, weiss für Werte, die gegen unendlich
gehen. Grafik: Mandelbrotmenge (s. Blatt "Mandelbrot") | ||
| "Strange Attractors", "Hopalong" | 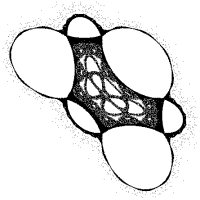 |
Diese Technik wird oft benutzt, um "strange attractors" das sind
grobübersetzt "seltsame Anziehungspunkte" von Chaotischen Systemen darzustellen.
Anstatt jedem Bildpunkt eine komplexe Zahl zuzuweisen, wird der umgekehrte
Weg benutzt: Man "verfolgt" einen Punkt durch die Iterationen und
zeichnet immer dort einen Punkt, wo er sich nach jeder Iteration befindet.
Deswegen wird diese Technik "hop-along" genannt, was soviel heißt
wie "weiterhüpfen", man schaut zu wie der Punkt hüpft. Grafik: Hopalong mit folgender Formel: xn+1 = yn - xn1/2 und yn+1 = 0.4 - xn Die Startkoordinaten x0 und y0 spielen, bis auf einige Ausnahmen, keine Rolle auf das endgültige Aussehen. | ||
| L-Systeme |  |
Lindenmayer-Systeme ergeben oft der Natur sehr nahestehende Grafiken,
und sind im Prinzip sehr leicht zu verstehen, und haben ein breites Anwendungsspektrum. | ||
| IFS-Systeme |  |
"Iterated Function Systems" werden ähnlich wie L-Systeme
gebildet, nur werden anstatt Linien Polygone verwendet und ineinander
eingesetzt. IFS-Systeme ermöglichen neue Wege in der Datenreduktion
für Bild-, Video- und Ton-Daten ("Fraktale Kompression").
| ||
| Newton-Rhapson | 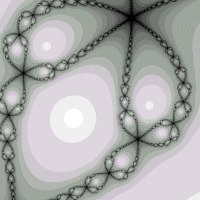 |
Ähnlich wie bei Chaotischen Systemen wird jedem Bildpunkt eine Koordinate
auf der Gausschen Zahlenebene zugewiesen. Mit der Newton-Rhapson Methode kann
man Nullstellen für ein beliebiges Polynom annähern. Jeder Bildpunkt,
und damit seine komplexe Zahl wird nun als Startwert für die Annäherung
gesetzt, und der Bildpunkt erhält, je nach dem wie schnell er konvergiert, eine
Farbe. Seltsam daran ist, das schon kleine Abweichungen beim Startwert einen
großen Unterschied bei der Geschwindigkeit der Konvergenz auslösen
können. Grafik: Polynom: z * z * z - 1 = 0, Ausschnitt des positiven Real- und Imaginärteils. |
| Name | URL |
|---|---|
| An Introduction into Fractals (knapp) | http://www.mhri.edu.au/~pdb/fractals/fracintro/ |
| Sci.Fractals Frequent Asked Questions | http://fractal.mta.ca/sci.fractals-faq/toc.html |
| Introduction into Chaos (ausführlich) | http://www.columbia.edu/~gae4/chaos/ |
| Sierpinski Triangle | http://www.students.uiuc.edu/~ag-ho/chaos/sierpinski.html |
| The Relation between PI and the Mandelbrot set | http://www.frii.com/~dboll/mandel.html |
| Fractal Art | http://www.fractals.com/fractal_gallery/uwe_krueger/room1.html |
| MicroSoft Encarta Encyclopädie 98 | - |